Twój bryk e-math.pl
Twoja lekcja jest w innej zakładce przeglądarki.
Klawiszologia czyli jak korzystać z klawiatury komputera przy pisaniu wzorów
| efekt | skrót klawiaturowy | znak na klawiszu | opis |
|---|---|---|---|
 |
/ | / | ułamek |
 |
shift + 6 | ^ | wykładnik potęgi (indeks górny) |
 |
shift + - | _ | indeks dolny |
 |
shift + / | ? | √ pierwiastek |
 |
shift + 3 | # | Δ delta |
 |
shift + 2 | @ | α alfa |
 |
shift + 7 | & | ° stopień |
 |
shift + 4 | $ | ∞ nieskończoność |
 |
shift + ' | " | π pi |
 |
shift + 1 | ! | silnia |
 |
shift + 5 | % | procent |
 |
shift + 8 | * | symbol mnożenia |
Notacja
| symbol | znaczenie |
|---|---|
| ∈ | należy |
| ∉ | nie należy |
| ⊂ | zawiera |
| ∪ | suma zbiorów |
| ∩ | iloczyn zbiorów |
| ∧ | i |
| ∨ | lub |
| ⇒ | jeżeli... to... |
| ⇔ | wtedy i tylko wtedy |
| a+b | suma | a · b = b · a | iloczyn | \[ \frac{a}{b} \] | iloraz |
Zbiory
Suma zbiorów
A∪B

Różnica zbiorów
A-B

Iloczyn zbiorów (część wspólna)
A∩B
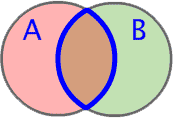
|A| = moc zbioru, czyli liczba elementów zbioru A
A = ∅ ⇔ |A| = 0
Ω - przestrzeń zdarzeń elementarnych
A - zdarzenie elementarne
A' - zdarzenie przeciwne do A
A' = Ω - A

Dzielniki
| czy dzieli się przez | liczba jest podzielna jeżeli |
|---|---|
| 1 | każda liczba jest podzielna przez 1 |
| 2 | ostatnia cyfra liczby to: 0, 2, 4, 6 lub 8 (liczby parzyste) |
| 3 | suma cyfr liczby podzielna jest przez 3 |
| 4 | liczba złożona z dwóch ostatnich cyfr jest podzielna przez 4, dzielisz ją przez 2 i sprawdzasz czy wynik jest parzysty |
| 5 | ostatnia cyfra to 5 lub 0 |
| 6 | jest podzielna przez 2 i przez 3, czyli parzysta i suma cyfr podzielna przez 3 |
| 8 | liczba złożona z trzech ostatnich cyfr dzieli się przez 8, tzn. dzielisz ją przez 2 i sprawdzasz czy dzieli się przez 4 |
| 9 | suma cyfr jest podzielna przez 9 |
Dziedzina
| Zapis działania | ograniczenia dziedziny przy danym działaniu |
|---|---|
| \[ \frac{f(x)}{g(x)} \] | \[ g(x) \neq 0 \] |
| \[ \sqrt[2n]{f(x)} \] | \[ f(x) \geqslant 0 \] |
| \[ tg f(x) \] | \[ f(x) \neq \frac{\pi}{2}+k\pi \] |
| \[ ctg f(x) \] | \[ f(x) \neq \pi + k \pi \] |
| \[ a^x \] | \[ a \gt 0 \] |
| \[ log_a{f(x)} \] | \[ f(x) \gt 0 \land a \gt 0 \land a \neq 1 \] |
Potęgi popularne i przydatne
potęgi
liczby 2
20 = 1
21 = 2
22 = 4
23 = 8
24 = 16
25 = 32
26 = 64
27 = 128
28 = 256
29 = 512
210 = 1024
potęgi
liczby 3
30 = 1
31 = 3
32 = 9
33 = 27
34 = 81
35 = 243
potęgi
liczby 5
50 = 1
51 = 5
52 = 25
53 = 125
54 = 625
55 = 3125
kwadraty
popularnych liczb
12 = 1
22 = 4
32 = 9
42 = 16
52 = 25
62 = 36
72 = 49
82 = 64
92 = 81
102 = 100
kwadraty
popularnych liczb
112 = 121
122 = 144
132 = 169
142 = 196
152 = 225
162 = 256
172 = 289
182 = 324
192 = 361
202 = 400
trzecie
potęgi
13 = 1
23 = 8
33 = 27
43 = 64
53 = 125
63 = 216
73 = 343
83 = 512
93 = 729
103 = 1000
Trygonometria
| α | 0 = 0° | \[ \frac{π}{6}=30°\] | \[ \frac{π}{4}=45°\] | \[ \frac{π}{3}=60°\] | \[ \frac{π}{2}=90°\] |
|---|---|---|---|---|---|
| sinα | 0 | \[ \frac{1}{2} \] | \[ \frac{\sqrt{2}}{2} \] | \[ \frac{\sqrt{3}}{2} \] | 1 |
| cosα | 1 | \[ \frac{\sqrt{3}}{2} \] | \[ \frac{\sqrt{2}}{2} \] | \[ \frac{1}{2} \] | 1 |
| tgα | 0 | \[ \frac{\sqrt{3}}{3} \] | 1 | \[ \sqrt{3} \] | nie istnieje |
| ctgα | nie istnieje | \[ \sqrt{3} \] | 1 | \[ \frac{\sqrt{3}}{3} \] | 0 |
Zbiory liczb
zbiór liczb naturalnych:
N = {0;1;2;3;4;5;6...}
zbiór liczb całkowitych:
C = {...-6;-5;-4;-3;-2;-1;0;1;2;3;4...}
zbiór liczb wymiernych (ułamki zwykłe):
\[ W=\frac{\text{liczba całkowita}}{\text{liczba całkowita} ≠ 0} \]
zbiór liczb niewymiernych:
IW = ułamki nieskończone nieokresowe
zbiór liczb rzeczywistych (wszystkie liczby jakie znasz):
R = W ∪ IW
(suma zbioru liczb wymiernych i niewymiernych)

R = R- + R+ + {0}
Przedrostki liczb
| przedrostek | wymowa | zapis | zapis |
|---|---|---|---|
| T | tera | 109 | 1 000 000 000 |
| M | mega | 106 | 1 000 000 |
| k | kilo | 103 | 1 000 |
| h | hekto | 102 | 100 |
| da | deka | 101 | 10 |
| 100 | 1 | ||
| d | decy | 10-1 | 0,1 |
| c | centy | 10-2 | 0,01 |
| m | mili | 10-3 | 0,001 |
| µ | mikro | 10-6 | 0,000 001 |
| n | nano | 10-9 | 0,000 000 001 |
Jednostki
| jednostka | wymowa | zapis | zapis |
|---|---|---|---|
| 1 t | 1 tona | 103 kg | 1 000 kg |
| 1 a | 1 ar | 102 m2 | 100 m2 |
| 1 ha | 1 hektar | 100 a | 104 m2 |
| 1 l | 1 litr | 1 dm3 | 10-3 m3 |
| jednostka | miara |
|---|---|
| para | 2 sztuki (2 szt.) |
| tuzin | 12 sztuk (12 szt.) |
| mendel | 15 sztuk (15 szt.) |
| kopa | 60 sztuk, 5 tuzinów, 4 mendle |
| mol | 6,02 · 1023 szt. |
| gugol | 10100 sztuk |
Rozkład

Pracuj z tablicami. Będziesz je mieć na maturze! Używaj na lekcji, klasówce.